How to Convert Radians to Degrees and Vice Versa?

Last updated: March 18, 2024

Reviewed by: Milos Simic

1. Overview

In this tutorial, we’ll review two standard angular units: the degree and the radian. First, we’ll provide their mathematical definitions. Then, we’ll explain how to convert radians to degrees and vice versa.

2. Degree

The degree is a unit of angular measurement defined as 1/360 of a round angle. It isn’t the recommended angle unit in the International System of Units (SI) but is commonly used in geometry. The symbol ^{\circ} denotes the degree unit.

The precise reason behind selecting degrees as the unit of measurement for rotations and angles remains uncertain. One hypothesis suggests a connection to the fact that 360 is roughly the number of days in a year.

3. Radian

The radian is the angular unit in the SI. To define the measure of angles in radians, we consider a circumference with center O and radius r. Let’s observe an angle \alpha in the center. Such an angle subtends an arc AB of length l:

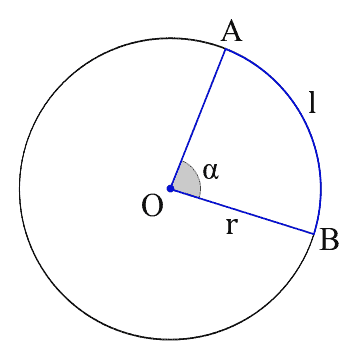
radian definition

The ratio of the arc length l and the radius r represents the measure of the angle \alpha expressed in radians, i.e.:

(1)   \begin{equation*} \alpha_{\text{rad}} = \frac{l}{r} \end{equation*}

Being the ratio between two lengths, the radian is a dimensionless quantity.

We can see its meaning in its definition. If we consider an angle equal to 1 radian, the corresponding arc length will equal the radius:

(2)   \begin{equation*} \alpha_{\mathrm{rad}}=1 \quad \Leftrightarrow \quad l=r \end{equation*}

In other words, the radian is the angle subtended at the center of a circle by an arc whose length is equal to the circle’s radius.

The symbol \text{rad} denotes the radian unit, but angles without any specified unit are generally assumed in radians.

4. Convert Radians to Degrees and Vice Versa

The following mathematical proportion is fundamental for the conversion between radians and degrees:

(3)   \begin{equation*} {\alpha_{\text{rad}} \over \pi} = {\alpha_{\text{deg}} \over 180^{\circ} } \end{equation*}

where \alpha_{\text{rad}}  denotes an angle expressed in radians and {\alpha_{\text{deg}} the corresponding one expressed in degrees.

Given the angle in radians \boldsymbol{ \alpha_{\text{rad}}}, the corresponding angle in degrees can be calculated as:

(4)   \begin{equation*} \alpha_{\text{deg}} = 180^{\circ} { \alpha_{\text{rad}} \over \pi} \end{equation*}

Conversely, to convert an angle in degrees \boldsymbol{\alpha_{\text{deg}}} to radians we compute:

(5)   \begin{equation*} \alpha_{\text{rad}} = \pi { \alpha_{\text{deg}} \over 180^{\circ} } \end{equation*}

5. Numerical Examples

Now, let’s express the angle of 1 \text{rad} in degrees:

    \[\frac{180^{\circ} \times 1}{\pi} = 57.296 ^{\circ}\]

Similarly, let’s convert 30^{\circ} to radians:

    \[\frac{\pi \times 30^{\circ}}{ 180^{\circ}} = 0.5236 \ \text{rad}\]

6. When to Use Radians or Degrees?

Whether to use radians or degrees to express angles depends on the context.

In everyday life, people prefer degrees to radians. Also, degrees are more common when dealing with angles related to building and design in fields such as engineering, construction, and architecture. The degree is also the standard unit for measuring latitude and longitude in geography.

However, radians can simplify many mathematical formulas and calculations. So, we use them more often in physics and trigonometry. For example, the radian is the natural unit for measuring angles when working with circular motion.

7. Conclusion

In this article, we reviewed the mathematical definitions of the degree and radian, the most common units for angular measurement in geometry. We explained that a simple mathematical proportion allows us to convert radians to degrees and vice versa. Radians are SI units for angles and are more used in maths and physics, whereas we prefer degrees in other fields and everyday life.

Comments are open for 30 days after publishing a post. For any issues past this date, use the Contact form on the site.