1. Overview
In this article, we’re going to discuss Minimax algorithm and its applications in AI. As it’s a game theory algorithm, we’ll implement a simple game using it.
We’ll also discuss the advantages of using the algorithm and see how it can be improved.
2. Introduction
Minimax is a decision-making algorithm, typically used in a turn-based, two player games. The goal of the algorithm is to find the optimal next move.
In the algorithm, one player is called the maximizer, and the other player is a minimizer. If we assign an evaluation score to the game board, one player tries to choose a game state with the maximum score, while the other chooses a state with the minimum score.
In other words, the maximizer works to get the highest score, while the minimizer tries get the lowest score by trying to counter moves.
It is based on the zero-sum game concept. In a zero-sum game, the total utility score is divided among the players. An increase in one player’s score results into the decrease in another player’s score. So, the total score is always zero. For one player to win, the other one has to lose. Examples of such games are chess, poker, checkers, tic-tac-toe.
An interesting fact- in 1997, IBM’s chess-playing computer Deep Blue (built with Minimax) defeated Garry Kasparov (the world champion in chess).
3. Minimax Algorithm
Our goal is to find the best move for the player. To do so, we can just choose the node with best evaluation score. To make the process smarter, we can also look ahead and evaluate potential opponent’s moves.
For each move, we can look ahead as many moves as our computing power allows. The algorithm assumes that the opponent is playing optimally.
Technically, we start with the root node and choose the best possible node. We evaluate nodes based on their evaluation scores. In our case, evaluation function can assign scores to only result nodes (leaves). Therefore, we recursively reach leaves with scores and back propagate the scores.
Consider the below game tree:
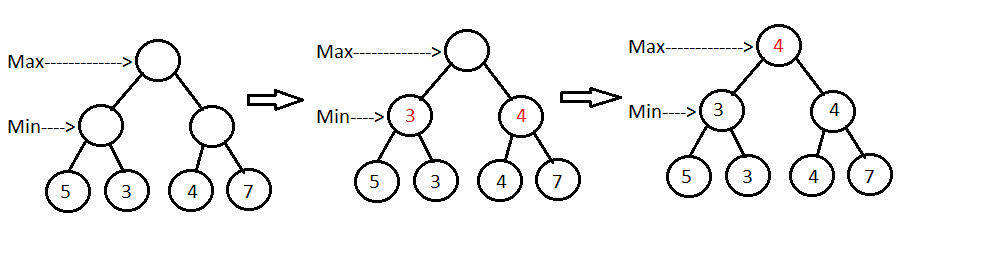
Maximizer starts with the root node and chooses the move with the maximum score. Unfortunately, only leaves have evaluation scores with them, and hence the algorithm has to reach leaf nodes recursively. In the given game tree, currently it’s the minimizer’s turn to choose a move from the leaf nodes, so the nodes with minimum scores (here, node 3 and 4) will get selected. It keeps picking the best nodes similarly, till it reaches the root node.
Now, let’s formally define steps of the algorithm:
- Construct the complete game tree
- Evaluate scores for leaves using the evaluation function
- Back-up scores from leaves to root, considering the player type:
- For max player, select the child with the maximum score
- For min player, select the child with the minimum score
- At the root node, choose the node with max value and perform the corresponding move
4. Implementation
Now, let’s implement a game.
In the game, we have a heap with n number of bones. Both players have to pick up 1,2 or 3 bones in their turn. A player who can’t take any bones loses the game. Each player plays optimally. Given the value of n, let’s write an AI.
To define the rules of the game, we will implement GameOfBones class:
class GameOfBones {
static List<Integer> getPossibleStates(int noOfBonesInHeap) {
return IntStream.rangeClosed(1, 3).boxed()
.map(i -> noOfBonesInHeap - i)
.filter(newHeapCount -> newHeapCount >= 0)
.collect(Collectors.toList());
}
}
Furthermore, we also need the implementation for Node and Tree classes as well:
public class Node {
int noOfBones;
boolean isMaxPlayer;
int score;
List<Node> children;
// setters and getters
}
public class Tree {
Node root;
// setters and getters
}
Now we’ll implement the algorithm. It requires a game tree to look ahead and find the best move. Let’s implement that:
public class MiniMax {
Tree tree;
public void constructTree(int noOfBones) {
tree = new Tree();
Node root = new Node(noOfBones, true);
tree.setRoot(root);
constructTree(root);
}
private void constructTree(Node parentNode) {
List<Integer> listofPossibleHeaps
= GameOfBones.getPossibleStates(parentNode.getNoOfBones());
boolean isChildMaxPlayer = !parentNode.isMaxPlayer();
listofPossibleHeaps.forEach(n -> {
Node newNode = new Node(n, isChildMaxPlayer);
parentNode.addChild(newNode);
if (newNode.getNoOfBones() > 0) {
constructTree(newNode);
}
});
}
}
Now, we’ll implement the checkWin method which will simulate a play out, by selecting optimal moves for both players. It sets the score to:
- +1, if maximizer wins
- -1, if minimizer wins
The checkWin will return true if the first player (in our case – maximizer) wins:
public boolean checkWin() {
Node root = tree.getRoot();
checkWin(root);
return root.getScore() == 1;
}
private void checkWin(Node node) {
List<Node> children = node.getChildren();
boolean isMaxPlayer = node.isMaxPlayer();
children.forEach(child -> {
if (child.getNoOfBones() == 0) {
child.setScore(isMaxPlayer ? 1 : -1);
} else {
checkWin(child);
}
});
Node bestChild = findBestChild(isMaxPlayer, children);
node.setScore(bestChild.getScore());
}
Here, the findBestChild method finds the node with the maximum score if a player is a maximizer. Otherwise, it returns the child with the minimum score:
private Node findBestChild(boolean isMaxPlayer, List<Node> children) {
Comparator<Node> byScoreComparator = Comparator.comparing(Node::getScore);
return children.stream()
.max(isMaxPlayer ? byScoreComparator : byScoreComparator.reversed())
.orElseThrow(NoSuchElementException::new);
}
Finally, let’s implement a test case with some values of n (the number of bones in a heap):
@Test
public void givenMiniMax_whenCheckWin_thenComputeOptimal() {
miniMax.constructTree(6);
boolean result = miniMax.checkWin();
assertTrue(result);
miniMax.constructTree(8);
result = miniMax.checkWin();
assertFalse(result);
}
5. Improvement
For most of the problems, it is not feasible to construct an entire game tree. In practice, we can develop a partial tree (construct the tree till a predefined number of levels only).
Then, we will have to implement an evaluation function, which should be able to decide how good the current state is, for the player.
Even if we don’t build complete game trees, it can be time-consuming to compute moves for games with high branching factor.
Fortunately, there is an option to find the optimal move, without exploring every node of the game tree. We can skip some branches by following some rules, and it won’t affect the final result. This process is called pruning. Alpha–beta pruning is a prevalent variant of minimax algorithm.
6. Conclusion
Minimax algorithm is one of the most popular algorithms for computer board games. It is widely applied in turn based games. It can be a good choice when players have complete information about the game.
It may not be the best choice for the games with exceptionally high branching factor (e.g. game of GO). Nonetheless, given a proper implementation, it can be a pretty smart AI.
As always, the complete code for the algorithm can be found over on GitHub.






